Injective hull

In mathematics, especially in the area of abstract algebra known as module theory, the injective hull (or injective envelope) of a module is both the smallest injective module containing it and the largest essential extension of it. Injective hulls were first described in (Eckmann & Schopf 1953), and are described in detail in the textbook (Lam 1999).

1 Definition
2 Properties
3 Examples
4 Uniform dimension and injective modules
5 Generalization
6 See also
7 External links
8 Notes
9 References

Definition

A module E is called the injective hull of a module M, if E is an essential extension of M, and E is injective. Here, the base ring is a ring with unity, though possibly non-commutative.

Properties

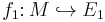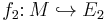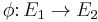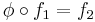Every module M has an injective hull which is unique up to isomorphism. To be explicit, suppose $f_1 \colon M \hookrightarrow E_1$ and $f_2 \colon M \hookrightarrow E_2$ are both injective hulls. Then there is an isomorphism $\phi \colon E_1 \to E_2$ such that $\phi\circ f_1 = f_2$ .

Examples

The injective hull of an injective module is itself.
The injective hull of an integral domain is its field of fractions, (Lam 1999, Example 3.35)
The injective hull of a cyclic p-group (as Z-module) is a Prüfer group, (Lam 1999, Example 3.36)
The injective hull of R/rad(R) is Hom_k(R,k), where R is a finite dimensional k-algebra with Jacobson radical rad(R), (Lam 1999, Example 3.41).
A simple module is necessarily the socle of its injective hull.

Uniform dimension and injective modules

An R module M has finite uniform dimension (=finite rank) n if and only if the injective hull of M is a finite direct sum of n indecomposable submodules.

Generalization

More generally, let C be an abelian category. An object E is an injective hull of an object M if M → E is an essential extension and E is an injective object. If C is locally small, satisfies Grothendieck's axiom AB5) and has enough injectives, then every object in C has an injective hull (these three conditions are satisfied by the category of modules over a ring).^[1]

External links

injective hull (PlanetMath article)
PlanetMath page on modules of finite rank

Notes

^ Section III.2 of (Mitchell 1965)

References

Eckmann, B.; Schopf, A. (1953), "Über injektive Moduln", Archiv der Mathematik 4 (2): 75–78, doi:10.1007/BF01899665, ISSN 0003-9268, MR 0055978
Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294
Matsumura, H. Commutative Ring Theory, Cambridge studies in advanced mathematics volume 8.
Mitchell, Barry (1965), Theory of categories, Pure and applied mathematics, 17, Academic Press, ISBN 978-0-124-99250-4, MR 0202787